Imagine that there are 1000 buttons on the floor, and you start connecting random pairs of them with thread. There's a beautiful phase transition that occurs if you plot "average links per button" vs. "fraction of buttons in largest connected group". The transition occurs at x=1.



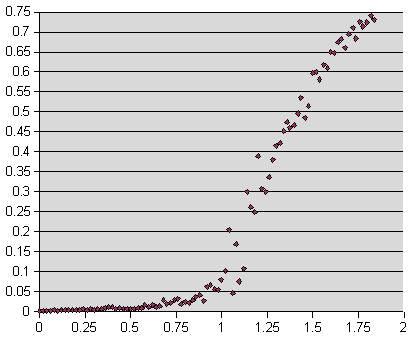
I learned of this phenomenon from the book Six Degrees which Yoz recommended. Here's the code I used to create the data for the graph above:

$last_component_name = 0

class Button
  attr_accessor :component_name
  attr_accessor :link_count
  def initialize
    @link_count = 0
  end
  def connect(other)
    return if self == other
    @link_count += 1
    other.link_count += 1
    if @component_name.nil? && other.component_name.nil?
      $last_component_name += 1
      @component_name = $last_component_name
      other.component_name = $last_component_name
    elsif @component_name.nil?
      @component_name = other.component_name
    elsif other.component_name.nil?
      other.component_name = @component_name
    else
      renameComponent(other.component_name, @component_name)
    end
  end
end

$buttons = []
1.upto(1000) do |i|
  $buttons << Button.new
end

def renameComponent(a, b)
  $buttons.each do |button|
    if button.component_name == a
      button.component_name = b
    end
  end
end

class Array
  def random
    at(rand(length))
  end
end

1.upto(ARGV[0].to_f * 1000) do |i|
  $buttons.random.connect($buttons.random)
end

max_tally = 0
max_tally_component_name = ''
component_name_to_frequency_hash = {}
$buttons.each do |button|
  if not button.component_name.nil?
    tally = component_name_to_frequency_hash[button.component_name]
    tally = tally.nil? ? 0 : (tally+1)
    component_name_to_frequency_hash[button.component_name] = tally
    if max_tally < tally
      max_tally = tally
      max_tally_component_name = button.component_name
    end
  end
end

fraction_in_largest_component = max_tally/(1.0*$buttons.size)

total_link_count = 0
$buttons.each do |button|
  total_link_count += button.link_count
end

average_link_count = total_link_count/(1.0*$buttons.size)

puts "#{average_link_count}, #{fraction_in_largest_component}"